Sensitivity analysis

Sensitivity analysis (SA) is the study of how the variation (uncertainty) in the output of a statistical model can be attributed to different variations in the inputs of the model.^[1] Put another way, it is a technique for systematically changing variables in a model to determine the effects of such changes.

In any budgeting process there are always variables that are uncertain. Future tax rates, interest rates, inflation rates, headcount, operating expenses and other variables may not be known with great precision. Sensitivity analysis answers the question, "if these variables deviate from expectations, what will the effect be (on the business, model, system, or whatever is being analyzed)?"

In more general terms uncertainty and sensitivity analysis investigate the robustness of a study when the study includes some form of statistical modelling. Sensitivity analysis can be useful to computer modelers for a range of purposes,^[2] including:

Support decision making or the development of recommendations for decision makers (e.g. testing the robustness of a result);
Enhancing communication from modellers to decision makers (e.g. by making recommendations more credible, understandable, compelling or persuasive);
Increased understanding or quantification of the system (e.g. understanding relationships between input and output variables); and
Model development (e.g. searching for errors in the model).

1 Overview
2 Methodology
3 Related concepts
4 Applications
5 See also
6 Notes
7 References
8 Further reading
9 External links

Overview

Statistical problems met in social, economic or natural sciences may entail the use of statistical models, which generally do not lend themselves to a straightforward understanding of the relationship between input factors (what goes into the model) and output (the model’s dependent variables). Such an appreciation, i.e. the understanding of how the model behaves in response to changes in its inputs, is of fundamental importance to ensure a correct use of the models.

A statistical model is defined by a series of equations, input factors, parameters, and variables aimed at characterizing the process being investigated.

Input is subject to many sources of uncertainty including errors of measurement, absence of information and poor or partial understanding of the driving forces and mechanisms. This uncertainty imposes a limit on our confidence in the response or output of the model. Further, models may have to cope with the natural intrinsic variability of the system, such as the occurrence of stochastic events.

Good modeling practice requires that the modeler provides an evaluation of the confidence in the model, possibly assessing the uncertainties associated with the modeling process and with the outcome of the model itself. Uncertainty and Sensitivity Analysis offer valid tools for characterizing the uncertainty associated with a model. Uncertainty analysis (UA) quantifies the uncertainty in the outcome of a model. Sensitivity Analysis has the complementary role of ordering by importance the strength and relevance of the inputs in determining the variation in the output.^[1]

In models involving many input variables sensitivity analysis is an essential ingredient of model building and quality assurance. National and international agencies involved in impact assessment studies have included sections devoted to sensitivity analysis in their guidelines. Examples are the European Commission, the White House Office of Management and Budget, the Intergovernmental Panel on Climate Change and US Environmental Protection Agency.

Sometimes a sensitivity analysis may reveal surprising insights about the subject of interest. For instance, the field of multi-criteria decision making (MCDM) studies (among other topics) the problem of how to select the best alternative among a number of competing alternatives. This is an important task in decision making. In such a setting each alternative is described in terms of a set of evaluative criteria. These criteria are associated with weights of importance. Intuitively, one may think that the larger the weight for a criterion is, the more critical that criterion should be. However, this may not be the case. It is important to distinguish here the notion of criticality with that of importance. By critical, we mean that a criterion with small change (as a percentage) in its weight, may cause a significant change of the final solution. It is possible criteria with rather small weights of importance (i.e., ones that are not so important in that respect) to be much more critical in a given situation than ones with larger weights.^[3]^[4] That is, a sensitivity analysis may shed light into issues not anticipated at the beginning of a study. This, in turn, may dramatically improve the effectiveness of the initial study and assist in the successful implementation of the final solution.

Methodology

There are several possible procedures to perform uncertainty (UA) and sensitivity analysis (SA). Important classes of methods are:

Local methods, such as the simple derivative of the output $Y$ with respect to an input factor $X_i$ :

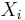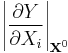$\left| \frac{\partial Y}{\partial X_i} \right |_{\textbf {x}^0 }$ ,

where the subscript 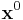$\textbf {x}^0$ indicates that the derivative is taken at some fixed point in the space of the input (hence the 'local' in the name of the class). Adjoint modelling^[5]^[6] and Automated Differentiation^[7] are methods in this class.

A sampling^[8]-based sensitivity is one in which the model is executed repeatedly for combinations of values sampled from the distribution (assumed known) of the input factors. Once the sample is generated, several strategies (including simple input-output scatterplots) can be used to derive sensitivity measures for the factors.
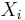Methods based on emulators (e.g. Bayesian^[9]). With these methods the value of the output $Y$ , or directly the value of the sensitivity measure of a factor $X_i$ , is treated as a stochastic process and estimated from the available computer-generated data points. This is useful when the computer program which describes the model is expensive to run.
Screening methods. This is a particular instance of sampling based methods. The objective here is to estimate a few active factors in models with many factors. One of the most commonly used screening method is the elementary effect method.^[10]^[11]
Variance based methods.^[12]^[13]^[14] Here the unconditional variance 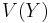$V(Y)$ of $Y$ is decomposed into terms due to individual factors plus terms due to interaction among factors. Full variance decompositions are only meaningful when the input factors are independent from one another.^[15]
High Dimensional Model Representations (HDMR).^[16]^[17] The term is due to H. Rabitz^[18] and include as a particular case the variance based methods. In HDMR the output $Y$ is expressed as a linear combination of terms of increasing dimensionality.
Methods based on Monte Carlo filtering.^[19]^[20] These are also sampling-based and the objective here is to identify regions in the space of the input factors corresponding to particular values (e.g. high or low) of the output.

Often (e.g. in sampling-based methods) UA and SA are performed jointly by executing the model repeatedly for combination of factor values sampled with some probability distribution. The following steps can be listed:

Specify the target function of interest.
- It is easier to communicate the results of a sensitivity analysis when the target of interest has a direct relation to the problem tackled by the model.
Assign a probability density function to the selected factors.
- When this involves eliciting experts' opinion this is the most expensive and time consuming part of the analysis.
Generate a matrix of inputs with that distribution(s) through an appropriate design.
- As in experimental design, a good design for numerical experiments^[21] should give a maximum of effects with a minimum of computed points.
Evaluate the model and compute the distribution of the target function.
- This is the computer-time intensive step.
Select a method for assessing the influence or relative importance of each input factor on the target function.
- This depends upon the purpose of the analysis, e.g. model simplification, factor prioritization, uncertainty reduction, etc.

Assumptions vs. inferences

In uncertainty and sensitivity analysis there is a crucial trade off between how scrupulous an analyst is in exploring the input assumptions and how wide the resulting inference may be. The point is well illustrated by the econometrician Edward E. Leamer (1990) ^[22]:

I have proposed a form of organized sensitivity analysis that I call ‘global sensitivity analysis’ in which a neighborhood of alternative assumptions is selected and the corresponding interval of inferences is identified. Conclusions are judged to be sturdy only if the neighborhood of assumptions is wide enough to be credible and the corresponding interval of inferences is narrow enough to be useful.

Note Leamer’s emphasis is on the need for 'credibility' in the selection of assumptions. The easiest way to invalidate a model is to demonstrate that it is fragile with respect to the uncertainty in the assumptions or to show that its assumptions have not been taken 'wide enough'. The same concept is expressed by Jerome R. Ravetz, for whom bad modeling is when uncertainties in inputs must be suppressed lest outputs become indeterminate.^[23]

Errors

In a sensitivity analysis, a Type I error is assessing as important a non-important factor and a Type II error is assessing as non-important an important factor. A Type III error corresponds to analysing the wrong problem, e.g. via an incorrect specification of the input uncertainties. Possible pitfalls in a sensitivity analysis are:

Unclear purpose of the analysis. Different statistical tests and measures are applied to the problem and different factors rankings are obtained. The test should instead be tailored to the purpose of the analysis, e.g. one uses Monte Carlo filtering if one is interested in which factors are most responsible for generating high/low values of the output.

Too many model outputs are considered. This may be acceptable for quality assurance of sub-models but should be avoided when presenting the results of the overall analysis.

Piecewise sensitivity. This is when one performs sensitivity analysis on one sub-model at a time. This approach is non conservative as it might overlook interactions among factors in different sub-models (Type II error).

The OAT paradox

In sensitivity analysis a common approach is that of changing one-factor-at-a-time (OAT), to see what effect this produces on the output. OAT customarily involves:^[24]

Moving one factor at a time and

Going back to the central/baseline point after each movement.

This appears a logical approach as any change observed in the output will unambiguously be due to the single factor changed. Furthermore by changing one factor at a time one can keep all other factors fixed to their central or baseline value. This increases the comparability of the results (all ‘effects’ are computed with reference to the same central point in space) and minimizes the chances of computer programme crashes, more likely when several input factors are changed simultaneously.^[24] The later occurrence is particularly annoying to modellers as in this case one does not know which factor's variation caused the model to crash.

The paradox is that this approach, apparently sound, is non-explorative, with exploration decreasing rapidly with the number of factors. With two factors, and hence in two dimensions, the OAT explores (partially) a circle instead of the full square (see figure). In this case one step along the abscissa moving from the origin, followed by a similar step along the ordinate—always moving from the origin, will leave us inside the circle and will never take us to the gray corners.

In k dimensions, the volume of the hyper-sphere included in (and tangent to) the unitary hyper-cube divided by that of the hyper-cube itself, goes rapidly to zero (e.g. it is less than 1% already for k = 10, see Figure). Note also that all OAT points are at most a distance one from the origin by design. 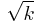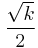Given that the diagonal of the hypercube is $\sqrt{k}$ in $k$ dimensions, if the points are distributed randomly there will be points (in the corners) which are distant from the origin $\frac{\sqrt{k}}{2}$ . In ten dimensions there are 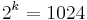$2^k=1024$ corners.

Latin hypercube sampling is often used in contexts where researchers feel the assumption of independent-uncertainty is too strong and it is desirable to explore corners of the factor-space.

Related concepts

While uncertainty analysis studies the overall uncertainty in the conclusions of the study, sensitivity analysis tries to identify what source of uncertainty weights more on the study's conclusions. For example, several guidelines for modelling (see e.g. one from the US EPA) or for impact assessment (see one from the European Commission) prescribe sensitivity analysis as a tool to ensure the quality of the modelling/assessment.

The problem setting in sensitivity analysis has strong similarities with design of experiments. In design of experiments one studies the effect of some process or intervention (the 'treatment') on some objects (the 'experimental units'). In sensitivity analysis one looks at the effect of varying the inputs of a mathematical model on the output of the model itself. In both disciplines one strives to obtain information from the system with a minimum of physical or numerical experiments.

Applications

Sensitivity analysis can be used

To simplify models

To investigate the robustness of the model predictions

To play what-if analysis exploring the impact of varying input assumptions and scenarios

As an element of quality assurance (unexpected factors sensitivities may be associated to coding errors or misspecifications).

It provides as well information on:

Factors that mostly contribute to the output variability

The region in the space of input factors for which the model output is either maximum or minimum or within pre-defined bounds (see Monte Carlo filtering above)

Optimal — or instability — regions within the space of factors for use in a subsequent calibration study

Interaction between factors

Sensitivity Analysis is common in physics and chemistry,^[25] in financial applications, risk analysis, signal processing, neural networks and any area where models are developed. Sensitivity analysis can also be used in model-based policy assessment studies . Sensitivity analysis can be used to assess the robustness of composite indicators ,^[26] also known as indices, such as the Environmental Performance Index.

Environmental

Computer environmental models are increasingly used in a wide variety of studies and applications. For example, global climate model are used for both short term weather forecasts and long term climate change.

Moreover, computer models are increasingly used for environmental decision making at a local scale, for example for assessing the impact of a waste water treatment plant on a river flow, or for assessing the behavior and life length of bio-filters for contaminated waste water.

In both cases sensitivity analysis may help understanding the contribution of the various sources of uncertainty to the model output uncertainty and system performance in general. In these cases, depending on model complexity, different sampling strategies may be advisable and traditional sensitivity indexes have to be generalized to cover multivariate sensitivity analysis, heteroskedastic effects and correlated inputs.

Business

In a decision problem, the analyst may want to identify cost drivers as well as other quantities for which we need to acquire better knowledge in order to make an informed decision. On the other hand, some quantities have no influence on the predictions, so that we can save resources at no loss in accuracy by relaxing some of the conditions. See Corporate finance: Quantifying uncertainty. Sensitivity analysis can help in a variety of other circumstances which can be handled by the settings illustrated below:

to identify critical assumptions or compare alternative model structures
guide future data collections
detect important criteria
optimize the tolerance of manufactured parts in terms of the uncertainty in the parameters
optimize resources allocation
model simplification or model lumping, etc.

However there are also some problems associated with sensitivity analysis in the business context:

Variables are often interdependent, which makes examining them each individually unrealistic, e.g.: changing one factor such as sales volume, will most likely affect other factors such as the selling price.
Often the assumptions upon which the analysis is based are made by using past experience/data which may not hold in the future.
Assigning a maximum and minimum (or optimistic and pessimistic) value is open to subjective interpretation. For instance one persons 'optimistic' forecast may be more conservative than that of another person performing a different part of the analysis. This sort of subjectivity can adversely affect the accuracy and overall objectivity of the analysis.

In modern econometrics the use of sensitivity analysis to anticipate criticism is the subject of one of the ten commandments of applied econometrics (from Kennedy, 2007^[27] ):

Thou shall confess in the presence of sensitivity. Corollary: Thou shall anticipate criticism [···] When reporting a sensitivity analysis, researchers should explain fully their specification search so that the readers can judge for themselves how the results may have been affected. This is basically an ‘honesty is the best policy’ approach, advocated by Leamer, (1978^[28]).

Chemical kinetics

With the accumulation of knowledge about kinetic mechanisms under investigation and with the advance of power of modern computing technologies, detailed complex kinetic models are increasingly used as predictive tools and as aids for understanding the underlying phenomena. A kinetic model is usually described by a set of differential equations representing the concentration-time relationship. Sensitivity analysis has been proven to be a powerful tool to investigate a complex kinetic model.^[29]^[30]

Kinetic parameters are frequently determined from experimental data via nonlinear estimation. Sensitivity analysis can be used for optimal experimental design, e.g. determining initial conditions, measurement positions, and sampling time, to generate informative data which are critical to estimation accuracy. A great number of parameters in a complex model can be candidates for estimation but not all are estimable. Sensitivity analysis can be used to identify the influential parameters which can be determined from available data while screening out the unimportant ones. Sensitivity analysis can also be used to identify the redundant species and reactions allowing model reduction.

In meta-analysis

In a meta analysis, a sensitivity analysis tests if the results are sensitive to restrictions on the data included. Common examples are large trials only, higher quality trials only, and more recent trials only. If results are consistent it provides stronger evidence of an effect and of generalizability.^[31]

Notes

^ ^a ^b Saltelli, A., Ratto, M., Andres, T., Campolongo, F., Cariboni, J., Gatelli, D. Saisana, M., and Tarantola, S., 2008, Global Sensitivity Analysis. The Primer, John Wiley & Sons.
^ Pannell, D.J. (1997). Sensitivity analysis of normative economic models: Theoretical framework and practical strategies, Agricultural Economics 16: 139-152.[1]
^ Triantaphyllou, E.; A. Sanchez (1997). "A Sensitivity Analysis Approach for Some Deterministic Multi-Criteria Decision-Making Methods". Decision Sciences 28 (1): 151–194. http://www.csc.lsu.edu/trianta/Journal_PAPERS1/SENSIT1.htm. Retrieved 2010-06-28.
^ Triantaphyllou, E. (2000). Multi-Criteria Decision Making: A Comparative Study. Dordrecht, The Netherlands: Kluwer Academic Publishers (now Springer). pp. 320. ISBN 0792366077. http://www.csc.lsu.edu/trianta/Books/DecisionMaking1/Book1.htm.
^ Cacuci, Dan G., Sensitivity and Uncertainty Analysis: Theory, Volume I, Chapman & Hall.
^ Cacuci, Dan G., Mihaela Ionescu-Bujor, Michael Navon, 2005, Sensitivity And Uncertainty Analysis: Applications to Large-Scale Systems (Volume II), Chapman & Hall.
^ Grievank, A. (2000). Evaluating derivatives, Principles and techniques of algorithmic differentiation. SIAM publisher.
^ J.C. Helton, J.D. Johnson, C.J. Salaberry, and C.B. Storlie, 2006, Survey of sampling based methods for uncertainty and sensitivity analysis. Reliability Engineering and System Safety, 91:1175–1209.
^ Oakley, J. and A. O'Hagan (2004). Probabilistic sensitivity analysis of complex models: a Bayesian approach. J. Royal Stat. Soc. B 66, 751–769.
^ Morris, M. D. (1991). Factorial sampling plans for preliminary computational experiments. Technometrics, 33, 161–174.
^ Campolongo, F., J. Cariboni, and A. Saltelli (2007). An effective screening design for sensitivity analysis of large models. Environmental Modelling and Software, 22, 1509–1518.
^ Sobol’, I. (1990). Sensitivity estimates for nonlinear mathematical models. Matematicheskoe Modelirovanie 2, 112–118. in Russian, translated in English in Sobol’ , I. (1993). Sensitivity analysis for non-linear mathematical models. Mathematical Modeling & Computational Experiment (Engl. Transl.), 1993, 1, 407–414.
^ Homma, T. and A. Saltelli (1996). Importance measures in global sensitivity analysis of nonlinear models. Reliability Engineering and System Safety, 52, 1–17.
^ Saltelli, A., K. Chan, and M. Scott (Eds.) (2000). Sensitivity Analysis. Wiley Series in Probability and Statistics. New York: John Wiley and Sons.
^ Saltelli, A. and S. Tarantola (2002). On the relative importance of input factors in mathematical models: safety assessment for nuclear waste disposal. Journal of American Statistical Association, 97, 702–709.
^ Li, G., J. Hu, S.-W. Wang, P. Georgopoulos, J. Schoendorf, and H. Rabitz (2006). Random Sampling-High Dimensional Model Representation (RS-HDMR) and orthogonality of its different order component functions. Journal of Physical Chemistry A 110, 2474–2485.
^ Li, G., W. S. W., and R. H. (2002). Practical approaches to construct RS-HDMR component functions. Journal of Physical Chemistry 106, 8721{8733.
^ Rabitz, H. (1989). System analysis at molecular scale. Science, 246, 221–226.
^ Hornberger, G. and R. Spear (1981). An approach to the preliminary analysis of environmental systems. Journal of Environmental Management 7, 7–18.
^ Saltelli, A., S. Tarantola, F. Campolongo, and M. Ratto (2004). Sensitivity Analysis in Practice: A Guide to Assessing Scientific Models. John Wiley and Sons.
^ Sacks, J., W. J. Welch, T. J. Mitchell, and H. P. Wynn (1989). Design and analysis of computer experiments. Statistical Science 4, 409–435.
^ Leamer, E., (1990) Let's take the con out of econometrics, and Sensitivity analysis would help. In C. Granger (ed.), Modelling Economic Series. Oxford: Clarendon Press 1990.
^ Ravetz, J.R., 2007, No-Nonsense Guide to Science, New Internationalist Publications Ltd.
^ ^a ^b Saltelli, A., Annoni, P., 2010, How to avoid a perfunctory sensitivity analysis, Environmental Modeling and Software 25, 1508-1517.
^ Saltelli, A., M. Ratto, S. Tarantola and F. Campolongo (2005) Sensitivity Analysis for Chemical Models, Chemical Reviews, 105(7) pp 2811–2828.
^ Saisana M., Saltelli A., Tarantola S., 2005, Uncertainty and Sensitivity analysis techniques as tools for the quality assessment of composite indicators, Journal Royal Statistical Society A, 168 (2), 307–323.
^ Kennedy, P. (2007). A guide to econometrics, Fifth edition. Blackwell Publishing.
^ Leamer, E. (1978). Specification Searches: Ad Hoc Inferences with Nonexperimental Data. John Wiley & Sons, Ltd, p. vi.
^ Rabitz, H., M. Kramer and D. Dacol (1983). Sensitivity analysis in chemical kinetics. Annual Review of Physical Chemistry, 34, 419–461.
^ Turanyi, T (1990). Sensitivity analysis of complex kinetic systems. Tools and applications. Journal of Mathematical Chemistry, 5, 203–248.
^ clinicalevidence.bmj.com > Glossary > sensitivity analysis Retrieved on June 21, 2010

References

Cruz, J. B., editor, (1973) System Sensitivity Analysis, Dowden, Hutchinson & Ross, Stroudsburg, PA.
Cruz, J. B. and Perkins, W.R., (1964), A New Approach to the Sensitivity Problem in Multivariable Feedback System Design, IEEE TAC, Vol. 9, 216-223.
Fassò A. (2007) Statistical sensitivity analysis and water quality. In Wymer L. Ed, Statistical Framework for Water Quality Criteria and Monitoring. Wiley, New York.
Fassò A., Esposito E., Porcu E., Reverberi A.P., Vegliò F. (2003) Statistical Sensitivity Analysis of Packed Column Reactors for Contaminated Wastewater. Environmetrics. Vol. 14, n.8, 743 - 759.
Fassò A., Perri P.F. (2002) Sensitivity Analysis. In Abdel H. El-Shaarawi and Walter W. Piegorsch (eds) Encyclopedia of Environmetrics, Volume 4, pp 1968–1982, Wiley.
Saltelli, A., S. Tarantola, and K. Chan (1999). Quantitative model-independent method for global sensitivity analysis of model output. Technometrics 41(1), 39–56.
Santner, T. J.; Williams, B. J.; Notz, W.I. Design and Analysis of Computer Experiments; Springer-Verlag, 2003.
Haug, Edward J.; Choi, Kyung K.; Komkov, Vadim (1986) Design sensitivity analysis of structural systems. Mathematics in Science and Engineering, 177. Academic Press, Inc., Orlando, FL.
Taleb, N. N., (2007) The Black Swan: The Impact of the Highly Improbable, Random House.
Pilkey, O. H. and L. Pilkey-Jarvis (2007), Useless Arithmetic. Why Environmental Scientists Can't Predict the Future. New York: Columbia University Press.

External links

Sixth Summer School on Sensitivity Analysis, Villa La Stella, Fiesole, Florence (ITALY) 14–17 September 2010
Sixth International Conference on Sensitivity Analysis of Model Output, Bocconi University, Milan (ITALY), 19–22 July 2010
Sensitivity analysis at the Joint Research Centre of the European Commission
- SimLab, the free software for global sensitivity analysis of the Joint Research Centre